|
|
|
|
|
|
01 |
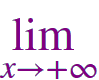 |
\(\cos x\) |
02 |
 |
\((\frac {x} {\sin x}\!+\!\frac {x} {\cos x}\!+\!\frac {x} {\tan x}) \) |
03 |
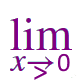 |
\(\large \frac{\cos x}{x}\) |
04 |
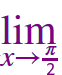 |
\(\large \frac {1-\sin x} {\cos^2 x} \; \) |
05 |
 |
\(\large \frac {\sin ax}{\sin bx}\) |
06 |
 |
\(\large \frac {\sin 4x \,\cdot\, \cos 2x} {\tan x} \) |
07 |
 |
\(\large \frac {\tan x}{4x}\) |
08 |
 |
\(\large \frac {\sin^2 x} {1-\,\cos x} \) |
09 |
 |
\(\large \frac {\sin^2 2x}{x^2}\) |
10 |
 |
\(\large \frac {\cos\,(\frac{\pi}{2}-x)} {x} \) |
11 |
 |
\(\large \frac{x}{\sin x\,+\,\tan x}\) |
12 |
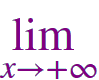 |
\(\left[x^2\cdot{\sin\frac{1}{x^2}}\right]\) |
13 |
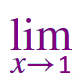 |
\(Bgtan\;x \) |
14 |
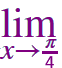 |
\(\large \frac {1\,+\;\tan x} {\sin x} \) |
30 |
 |
\(\large\frac {\cot x} {x} \) |
31 |
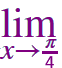 |
\(\large\frac{1\,-\,\tan x}{\sin x\,-\,\cos x} \)  |
32 |
 |
\( \cot x \) |
33 |
 |
\(\cos x \) (ook x→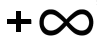 ) ) |
34 |
 |
\( {x\!\cdot\!\cot \frac x2} {} \) |
35 |
 |
\(\large \frac {\tan 6x} {\sin 2x \cdot \cos 3x} \) |
36 |
 |
\(\large \frac {\cos x\,-\,-x} {|x|} \) |
37 |
 |
\(\large \frac {\cos 2x - \cos x} {\sin^2 x} \) |
38 |
 |
\(\large \frac {\sin 2x} {\cos 3x} \) |
39 |
 |
\( \sin 2x \cdot \tan 3x \) |
40 |
 |
\(\large \frac {\cot 2x} {\cot x} \) |
41 |
 |
\(\large \frac {\sin^2 x\,+\,\tan^2 3x} {x^2} \) |
42 |
 |
\(2x \cdot \cot 2x \) |
30 |
 |
\(\large \frac {x+\sin 2x + \tan 3x} {x - \tan 2x} \) |
43 |
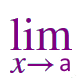 |
\(\large \frac {\cos x - \cos a} {x\,-\,a} \) |
44 |
 |
\(\large \frac {\cos 2x - \cos 2a} {\cos x - \cos a} \) |
45 |
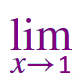 |
\(\large \frac {\sin x - \sin 1} {x\,-\,1} \) |
30 |
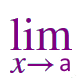 |
\(\large \frac {\sin x - \sin a} {x\,-\,a} \) |
46 |
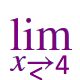 |
\(\large \frac {\sin x - \sin 4} {(x\,-\,4)^2} \) |
47 |
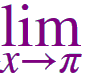 |
\(\large \frac {\sin x - \sin \pi} {x\,-\,\pi} \) |
48 |
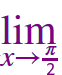 |
\(\large \frac {x - \frac {\pi}{2}} {\cos x} \) |
49 |
 |
\(\large 64^{\frac {sin^2 x} {\tan 2x}} \) |
50 |
 |
\(\large \frac {\sin^2 3x} {5x} \) |
51 |
 |
\(\large \frac {\sin^5 2x} {4x^5} \) |
52 |
 |
\(\large \frac {\sin x^{\circ}} {x} \) |
53 |
 |
\(wait \) |
54 |
 |
\(\large \frac {2x - \pi} {\cot x} \) |
55 |
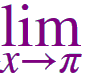 |
\(\large \frac {x\,-\,\pi} {\sin x} \) |
56 |
 |
\(\large \frac {x\,+\,\sin 2x} {x\,-\,\tan 2x} \) |
57 |
 |
\(\large \frac {x\,-\,\tan x} {x\,-\,\sin x} \) |
58 |
 |
\(\large \frac {x\,-\,\sin 2x} {x\,-\,\sin 3x} \) |
59 |
 |
\(\large \frac {x\,+\,\sin 2x} {x\,+\,\sin x} \) |
60 |
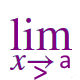 |
\(\large \frac {\tan x\,-\,\tan x} {x\:-\:a} \) |
61 |
 |
\(\large \frac {1\,-\,\cos 4x} {\cos 2x \,-\,1} \) |
62 |
 |
\(\large \frac {\large 1\,-\,\cos 2x} {1\,-\,\cos x} \) |
63 |
 |
\(\large \frac {\cos 16x\,-\,1} {1\,-\cos 4x} \) |
64 |
 |
\(\large \frac {1\:-\:\cos x} {x^2} \) |
65 |
 |
\(\large \frac {\cos ax\:-\:1} {x^2} \) |
66 |
 |
\(\large \frac {x\,\cdot\,\sin x} {1\:-\:\cos x} \) |
67 |
 |
\(\large \frac {x\:+\:\tan x} {1\,+\,x\,-\,\cos x} \) |
68 |
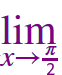 |
\(\large \frac {\sin \frac{\pi}{3}\,-\,\sin x} {\cos\frac{\pi}{3}\,-\,\cos x} \) |
69 |
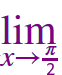 |
\(\large \frac {\cos x} {\pi\:-\:2x} \) |
70 |
 |
\(\large \frac {2x} {\sin x\:-\:x} \) |
71 |
 |
\(\large \frac {\sin^2x\,+\,1\,-\,\cos x} {x^2} \) |
72 |
 |
\(\large \frac {x\,\cdot\,\sin 2x} {1\,-\,\cos 3x} \) |
73 |
 |
\(\large \frac {\cos x\:-\:1} {x} \) |
74 |
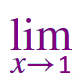 |
\(\large \frac {\tan \pi x} {1\:-\:x} \) |
75 |
 |
\(\large \frac {\sin^2 5x\,\cdot\,\cos 3x} {\tan^22x} \) |
76 |
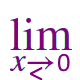 |
\(\large \left (\!\!\frac{\left | x \right |}{\sin x}\!+\!\frac{\left | x \right|\!}{\cos x}\!\! \right )\) |
77 |
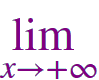 |
\(\large \frac {\cos \frac 1x \,-\,1} {\frac {1}{x^2}} \) |
78 |
 |
\( (x\cdot\cos x\cdot\cot x\,)\) |
79 |
 |
\((x^2.\csc 2x.\cot 2x) \) |
80 |
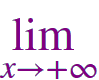 |
\( Bgtan\;x \) |
81 |
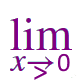 |
\(\ln \tan x \) |
82 |
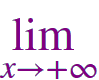 |
\(Bgtan \:e^x \) |
83 |
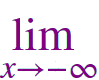 |
\(Bgtan \:e^x \) |
84 |
 |
\(\large f(x)\;=\;1\) |
85 |
 |
\((\cot x . Bgsin\:x)\) |
86 |
limiet |
\( Correct\:?\;(1) \) |
87 |
limiet |
\(Correct\:? \;(2) \) |
88 |
 |
\(\large \frac {x^2} {1\:-\:\sec 2x} \) |
89 |
 |
\(\large \frac{4x.\sin^23x}{\cos5x.\tan^32x}\) |
90 |
 |
\(\large \frac {1-\,\cos x\,+\, x^2}{1\:-\:\cos x} \) |
91 |
 |
\(\large \frac {3.Bgtan \:x\,-\:x}{2x\,-\,Bgsin \:x} \) |
92 |
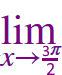 |
\(\large \frac {1\,+\:\sin x}{\cos^2x}\) |
93 |
 |
\(\large \frac {1\,-\,\sqrt{1\,-\,\sin x}} {x} \) |
94 |
 |
\(\large \frac {\cos^3\!x\,-\,1} {x^2.\,\cos^2x} \)  |
95 |
 |
\((\frac {x} {\sin x}\!+\!\frac {x} {\cos x}\!+ \!\frac {x} {\tan x}\!+\!\frac {x} {\cot x}) \) |
95 |
 |
\(\large \frac {\ln x - \ln \sin x} {x^2} \)  |
96 |
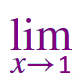 |
\((1-x).\tan\frac{\pi x}{2}\) |
97 |
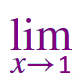 |
\(\large\frac{\sin(x-1)}{x^2-1} \)  |
98 |
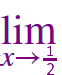 |
\(\small \left [ (4x^2\!-\!1).\cot(2x\!-\!1) \right ]\)  |
99 |
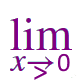 |
\(\large\frac{\log x}{\cot x}\)  |
100 |
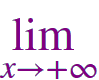 |
\( 2x\sin\frac 4x\)  |
A0 |
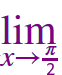 |
\(\large \frac {\tan \,3x} {\tan \,5x} \) |
A1 |
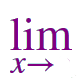 |
\(\large \frac {\cos 3x} {\cos x} \) (2 limieten) |
A2 |
 |
\(\large \frac {1\,-\,\cos 2x} {1\:-\:\frac{\sin x}{x}} \) |
A3 |
 |
\(\large \frac {1-\,\cos 2x.\cos x} {1\:-\:\cos x} \) |
A4 |
 |
\(\large \frac {1\,-\,\cos 3x} {1\:-\:\frac{\sin x}{x}} \) |
A5 |
 |
\(\large \frac {\tan x \: - \: \sin x} {x^3} \) |
A6 |
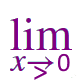 |
\((\cot \,x)^x\) |
A7 |
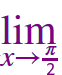 |
\((\sin 3x.\cos x.\tan 3x) \) |
A8 |
 |
\(\large \frac {1\,-\,\cos 4x} {\tan^2 3x} \) |
A9 |
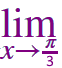 |
\(\left ( \sin \frac{\pi}{3} - \sin x \right).\tan \frac{3x}{2} \) |
B0 |
 |
\(\large \frac {x\:+\:\sin 2x} {x^2\,+\:\tan x} \) |
B1 |
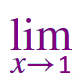 |
\(\large \frac {Bgcos\:x} {\sqrt{2\,-\,2x}} \) |
B2 |
 |
\(\large \frac {\sin x\:-\:\tan x} {\sin x\:-\:x} \) |
B3 |
 |
\( \left ( \frac{1\,-\,\cos 3x}{1-\,\cos x} -\frac{1-\,\cos 2x}{1-\,\cos x} \right ) \) |
B4 |
 |
\(\large \frac {x\,-\,x\cos x} {x\,-\,\sin x} \) |
B5 |
 |
\(\large \frac {1-\cos 2x} {x^2} vs. \frac{1-\cos x}{x^2} \) |
B6 |
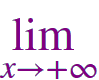 |
\(\large \frac {\cos \frac1x -1} {\frac{1}{x^2}} \) |
B7 |
 |
\(\large \frac {x} {D\frac{x}{\sin x}} \) |
B8 |
 |
\(\large \frac {x\,-\,Bgtan\:x} {x\,-\,\sin x} \) |
B9 |
 |
\(\large \frac {2\sin x - \sin 2x} {x\:-\:\sin x} \) |
C0 |
 |
\(\large \frac {x\:-\sin x} {x^3} \) |
C1 |
 |
\(\large (\cos x)^{\frac{1}{x^2}} \) |
C2 |
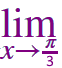 |
\(\large \frac {\sin (x-\frac{\pi}{3})} {1-2.\cos x} \) |
C3 |
 |
\(\large (\frac {\sin x} {x})^{\frac{1}{x^2}} \) |
C2 |
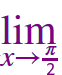 |
\(\large \frac {\sin x\,+\,\cos 2x} {1\,-\,\sin x} \) |
C4 |
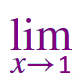 |
\(\left [ (x-1).\tan \frac{\pi x}{2} \right ] \) |
C4 |
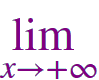 |
\((\tan \alpha)^x= \)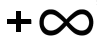 |
C5 |
 |
\(\large \frac {(3x\,-\,1)^8-\,(x\,-\,1)^8} {\sin x} \) |
C6 |
 |
\(\large \frac {\ln\:(1\,-\,x^2)} {\ln \cos x} \) |
C7 |
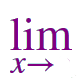 |
\(\large f(x) = \large \frac {1}{1-\sin x-\cos x} \) |
C8 |
 |
\(\large \frac {\tan x} {x^n}\small ∈\;\)
 |
C9 |
 |
\(\large \frac{1-\,\cos x\,+\,x.\sin x}{2x^2} \)  |