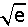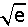^{\frac{1}{x^2}}=)
zeer moeilijk !
|
A. 1 |
|---|
| B. e |
C. 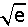 |
| D. \(\boldsymbol {\sqrt[3]{e}} \) |
| E. \(\boldsymbol {\sqrt[6]{e}} \) |
[ 6-8654 - op net sinds 20.4.2022-(E)-7.11.2023 ]
Translation in E N G L I S H
Oplossing - Solution
We steunen op : eln x = x, ln ya = a.ln y en \(\small\displaystyle \lim_{x \to 0} \:\frac {\tan x} {x}=1 \)
De limiet is dus ook gelijk aan
\(\large \displaystyle \lim_{x \to 0} \: e^{\frac {1} {x^2}.\ln \frac{\tan x}{x}} \)
Het komt er nu dus op aan van de limiet te zoeken van de exponent.
Dit is echter een onbepaalde vorm want zowel x2 als \(\ln \frac {\tan x}{x} \) naderen tot 0 als x → 0.
We gaan daarom beroep doen op de regel van de L'Hospital :
meerdere keren . . . vervolg later