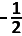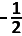Wiskunde Multiple Choice Vraag uit Gricha's Wiskundige Vragenbank

$https://latex.codecogs.com/png.image?\dpi{110}\displaystyle \lim_{x \to 0}\: \frac {\cos^3\!x\,-\,1} {x^2.\,\cos^2x}=$	A. − 2
B. −
C. − 1
D.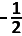
E. een positief getal

1^ste manier : met de regel van de l'Hospital
$\displaystyle\lim_{x\to 0}\frac{\cos^3x-1}{x^2.\cos^2x}\left(=\frac00\right)\buildrel H\over=\displaystyle\lim_{x\to 0}\frac{3\cos^2x.(-\sin x)}{2x.\cos^2x-2x^2.\cos x.\sin x}\\=-\frac32\displaystyle\lim_{x\to 0}\frac{\sin x.\cos x}{x.\cos x-x^2\sin x}=-\frac32\displaystyle\lim_{x\to 0}\frac{1}{\frac{x.\cos x-x^2.\sin x}{\sin x.\cos x}}\\=-\frac32\displaystyle\lim_{x\to 0}\frac{1}{\frac{x}{\sin x}-\frac{x^2}{\cos x}}=-\frac32.\frac{1}{1-0}=-\frac32$
2^de manier : zonder de regel van de l'Hospital
$\\\displaystyle\lim_{x\to 0}\frac{\cos^3x-1}{x^2.\cos^2x}=\displaystyle\lim_{x\to 0}\frac{\cos x-1}{x^2}.\displaystyle\lim_{\to 0}\frac{\cos^2x+\cos x+1}{\cos^2x}\\\\=\displaystyle\lim_{x\to 0}\frac{-2sin^2\frac x2}{x}.\frac{1+1+1}{1}=-2.\frac14.3=-\frac32$
3^de manier : met "een beetje" de regel van de l'Hospital
$\\\displaystyle\lim_{x\to 0}\frac{\cos^3x-1}{x^2.\cos^2x}=\displaystyle\lim_{x\to 0}\frac{\cos x-1}{x^2}.\displaystyle\lim_{x\to 0}\frac{\cos^2x+\cos x+1}{\cos^2x}\\\\\left(=\frac00\right)\buildrel H\over=\displaystyle\lim_{x\to 0}\frac{-\sin x}{2x}.\frac{1+1+1}{1}=-\frac12.3=-\frac32$