|
A. 1 |
|---|
| B. 2 |
| C. 3 |
| D. 0 |
E.  |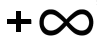
[ 5-2389 - op net sinds 16.6.12-(E)-4.11.2023 ]
Translation in E N G L I S H
|
A. 1 |
|---|
| B. 2 |
| C. 3 |
| D. 0 |
| E. ∞ |
Oplossing - Solution
1ste manier : zonder de regel van de L'Hospital
}{(1-\cos&space;x)(1+\cos&space;x)}\\=1+\lim_{x\to&space;0}\frac{x^2(1+\cos&space;x)}{1-\cos^2x}=1+\lim_{x\to&space;0}\frac{1+\cos&space;x}{\frac{\sin^2x}{x^2}}=1+\lim_{x\to&space;0}\frac{1+\cos&space;x}{\frac{\sin&space;x}{x}.\frac{\sin&space;x}{x}}=1+\frac{1+\cos&space;0}{1.1}\\=1+2=3 "\\\lim_{x\to 0}\frac{1\!-\cos x\,+\,x^2}{1\:-\:\cos x}=\lim_{x\to 0}\frac{1\!-\!\cos x}{1\!-\!\cos x}+\lim_{x\to 0}\frac{x^2}{1-\cos x}=1+\lim_{x\to 0}\frac{x^2(1+\cos x)}{(1-\cos x)(1+\cos x)}\\=1+\lim_{x\to 0}\frac{x^2(1+\cos x)}{1-\cos^2x}=1+\lim_{x\to 0}\frac{1+\cos x}{\frac{\sin^2x}{x^2}}=1+\lim_{x\to 0}\frac{1+\cos x}{\frac{\sin x}{x}.\frac{\sin x}{x}}=1+\frac{1+\cos 0}{1.1}\\=1+2=3")
2de manier : met de regel van de L'Hospital
\overset{H}{=}1+\lim_{x\to&space;0}\frac{2x}{0+\sin&space;x}\\=1+2.\lim_{x\to&space;0}\frac{x}{\sin&space;x}=1+2.1=3 "\\\lim_{x\to 0}\frac{1\!-\cos x\,+\,x^2}{1\:-\:\cos x}=\lim_{x\to 0}\frac{1\!-\!\cos x}{1\!-\!\cos x}+\lim_{x\to 0}\frac{x^2}{1-\cos x}\left(=1+\frac00\right)\overset{H}{=}1+\lim_{x\to 0}\frac{2x}{0+\sin x}\\=1+2.\lim_{x\to 0}\frac{x}{\sin x}=1+2.1=3")
3de manier : met de regel van de L'Hospital
\overset{H}{=}\lim_{x\to&space;0}\frac{\sin&space;x+2x}{\sin&space;x}=1+2.\lim_{x\to&space;0}\frac{x}{\sin&space;x}=1+2.1=3 "\\\lim_{x\to 0}\frac{1\!-\cos x\,+\,x^2}{1\:-\:\cos x}\left(=\frac00\right)\overset{H}{=}\lim_{x\to 0}\frac{\sin x+2x}{\sin x}=1+2.\lim_{x\to 0}\frac{x}{\sin x}=1+2.1=3")
