statistiek11
E(X) discreet, formule12
E(Z) en σ(Z)13
\(\small \displaystyle \sum_{i=1}^{n}\: (\mu\, x_i)\)14
xi → xi + 415
Σ Σ Σ Σ Σ16
N (x̄,σ)17
over x̄, σ en %18
E (X + 3) var (X + 3) 19
standaardafwijking 20
discrete toevalsveranderlijke21
z-verdeling 
22
30
\(\int_{-\infty}^{+\infty}e^{-\, \frac{\, x^2}{2}}\: dx \)31
continu - uniform32
standaardafwijking schatten33
standaardafwijking schatten34
standaardafw. berekenen35
standaardafwijking36
σ ; 20 muntstukken37
var(X) discreet+uniform38
kansvariabele X39
kansdichtheidsf. f(x)=k.(x+2)40
correctie van GAUSS41
Binom. → Norm. Verdeling42
buigpunt \(y=e^{-\, \frac{(x\,-\,1)^2}{2}}\)43
'quitte' met 1 dobbelsteen44
X discreet, parameter45
X discreet Z=2X46
Bernoulli_147
Bernoulli_248
Bernoulli_350
\(\int_{-\infty}^{+\infty}e^{-\, x^2}\: dx\)51
geldige kansdichtheidsfunctie52
E(X) discreet,uniform53
uniforme verd. - E(X)54
E(X) van f(x) =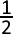 
sin x55
E(X) van verschil dobbelst.56
E(X) van grootste van vier57
E(X) van grootste van vijf58
E(X) bij meerkeuzevragen59
dobbelstenen E(X) = σ(X)60
E(X) - grootste - 2 d.s.61
E(X) - grootste - 3 d.s.62
E(X) - grootste - 2 uit 1063
E(X) - brieven(bussen) 70
N → P ( Z > -1 )71
N → P ( -
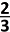< Z < 0 )72
N → P ( -2 < Z < +3 )73
N → P ( 1 < Z < 2 )74
N → P (Z < -2 )75
N → P (Z > 
)76
N → P ( Z > -0,7 )77
N → P ( | Z | < 2 )78
N → P ( | Z | > 1,6 )79
N → P ( | Z | > 0,9 )