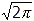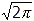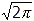De bepaalde integraal

is gelijk aan
|
A. 1 |
|---|
B.  |
C. 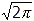 |
D.  |
E. 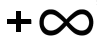 |
[ 6-7934 - op net sinds 25.5.15-(E)-10.6.2024 ]
Translation in E N G L I S H

is equal to
|
A. 1 |
|---|
B.  |
C. 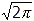 |
D.  |
| E. \(\infty\) |
Oplossing - Solution
De kansdichtheidsfunctie van de normale verdeling N(μ,σ) is
\(f(x)=\frac{1}{\sqrt{2\pi}}e^{-\frac{1}{2}\left(\frac{x-\mu}{\sigma}\right)^2}\)
en in het bijzonder voor μ = 0 en σ = 1 :
\(f(x)=\frac{1}{\sqrt{2\pi}}e^{-\frac{1}{2}x^2}=\frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}}\)
Aangezien nu voor elke kansdichtheidsfunctie (met domein IR )
moet gelden dat
\(\int_{-\infty}^{+\infty}{\frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}}}\;dx=1\), is het antwoord op de
vraag hieruit gemakkelijk af te leiden.