Welke waarde moet de
constante C hebben opdat
=C.\frac{1}{1+x^2}\quad&space;(x&space;\in&space;\mathbb{R}))
een geldige kansdichtheids-
functie zou zijn ?
constante C hebben opdat
een geldige kansdichtheids-
functie zou zijn ?
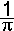
van C kan f een geldige
kansdichtheidsfunctie
zijn
|
Welke waarde moet de
constante C hebben opdat een geldige kansdichtheids- functie zou zijn ? |
A. 1 |
|---|---|
| B. 2 | |
| C. π | |
D. 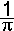 | |
| E. voor geen enkele waarde van C kan f een geldige kansdichtheidsfunctie zijn |
[ 6-7656 - op net sinds 21.3.2020-(E)-4.12.2023 ]
|
IN CONSTRUCTION |
A. |
|---|---|
| B. | |
| C. | |
| D. | |
| E. |
