Een discrete toevalsveranderlijke X
heeft 3 getalwaarden: 1, 2 en 3.
De kans dat X één van die 3 waarden
aanneemt is resp.  k2, 1 − k2, 1 −  k, 1 − k, 1 − 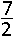 k2. k2.
Wat is de enige waarde die k kan aannemen ?
|
A. 1 |
|---|
| B. 2 |
| C. − 0,75 |
| D. 0 |
| E. 0,5 |
| F. − 0,6 |
[ 4-3993 - op net sinds 13.6.15-(E)-4.12.2023 ]
Translation in E N G L I S H
|
IN CONSTRUCTION
|
A. |
|---|
| B. |
| C. |
| D. |
| E. |
Oplossing - Solution
De som van de drie kansen moet gelijk zijn aan 1 !
\(\\\frac12k^2+(1-\frac12k)+(1-\frac72k^2)=1\\
\Leftrightarrow \;k^2+2-k+2-7k^2=2\\
\Leftrightarrow \;-6k^2-k+2=0 \)
De discriminant is D = 1 − 4.(−12) = 49 en de oplossingen
\(k_1=\frac{1+7}{-12}=\frac{8}{-12}=-\frac23\qquad
k_2=\frac{1-7}{-12}=\frac{-6}{-12}=-\frac12 \)
Toch kan de eerste breuk niet in aanmerking genomen worden.
Immers dan zou
\(1-\frac12k=1+\frac13=\frac43>1\)
en een kans kan nooit groter zijn dan 1.
Met de breuk \(\frac12\) worden de drie kansen \(\frac18,\;\frac34\;en\;\frac18\)
(met som 1 en alle drie tussen 0 en 1 !)