Stel dat X een continue kansvariabele is met
kansdichtheidsfunctie
f (x) =  .sin x .sin x
en domein [ 0, π ].
De verwachtingswaarde E(X) is dan
|
A. 1 |
|---|
B.  |
| C. π |
D. 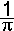 |
E.  |
[ 6-6587 - op net sinds 1.5.13-(E)-16.12.2023 ]
Translation in E N G L I S H
X is a continuous random variable
with probability density function
given by f (x) =  sinx sinx
on the domain [ 0, π ].
What is the expected value of X ?
|
A. 1 |
|---|
B.  |
| C. π |
D. 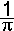 |
E.  |
Oplossing - Solution
1ste manier :
De verwachtingswaarde E(X) van een continue kansdichtheidsfunctie f met domein [a,b]
is \(\int_{a}^{b}{x.f(x)\;dx}\). (Vergelijk dat met de formule
\(\displaystyle \sum_{i=1}^{n}{x_i.f(x_i)} \)
voor een discrete kansfuntie f (merk de sterke gelijkenis op ! )
In ons geval wordt dat :
\( \int_{0}^{\pi}{x.\frac{1}{2}.\sin{x}\:dx}=\frac{1}{2}\int_{0}^{\pi}{x.\sin{x}\;d(-\cos{x})}\\
\buildrel P.I.\over= \frac{1}{2}\left[-x\cos{x}+\int_{0}^{\pi}{\cos{}\:dx}\right]_0^\pi
=\frac{1}{2}\left[-xcos{x}+sin{x}\right]_0^\pi=\frac{1}{2}\left[-\pi(-1)\right]=\frac{\pi}{2}\)
2de manier :
Daar de grafiek van y = sin x en dus ook van \(y=\frac12 \sin x \) bekend is en o.a. als nulwaarden 0 en π heeft, moet de verwachtingswaarde precies in het midden van het interval [ 0, π ] liggen.

 .sin x
.sin x
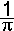

 .sin x
.sin x
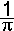

 sinx
sinx