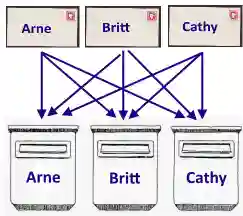
 Drie brieven zijn geadresseerd aan drie verschillende personen : Arne, Britt en Cathy.
Drie brieven zijn geadresseerd aan drie verschillende personen : Arne, Britt en Cathy.
De brieven worden willekeurig in een brievenbus gepost, één brief per brievenbus.
Het kan dus zijn dat geen enkele brief juist terecht komt maar ook dat alle brieven in de correcte brievenbus terecht komt.
Noem X de stochast (ook kansvariable of toevalsveranderlijke genoemd) die het aantal juiste toewijzingen weergeeft. (X is dus minstens 0 en hoogstens 3).
Als men dit experiment meerdere keren uitvoert, wat is dan het gemiddelde van het aantal juiste toewijzingen, m.a.w. wat is de verwachtingswaarde E(X)?
|
A. 1 |
|---|
| B. 2 |
| C. \(\frac12\) |
| D. \(\frac32\) |
| E. \(\frac43\) |
[ 6-8358 - op net sinds 22.4.2018-(E)-24.6.2025 ]
Translation in E N G L I S H
Three letters are addressed to three different persons : Arne, Britt & Cathy.
The letters are randomly posted in the mailbox, one letter per mailbox.
It is therefore possible that no letter arrives correctly, but also that all letters end up in the correct mailbox.
Name X the stochast that represents the number of correct assignments.
Therefore X is minimum 0 (no letter is in its proper mailbox ) and maximum 3 (all letters is in its proper mailbox)
What is the expectation value E(X) ?
|
A. 1 |
|---|
| B. 2 |
| C. \(\frac12\) |
| D. \(\frac32\) |
| E. \(\frac43\) |
Oplossing - Solution
De drie brieven voor A,B,C kunnen op 6 (=3!) manieren worden gepermuteerd.
Slechts één manier levert 3 correcte toewijzingen, nl. A-B-C
Geen enkel correcte toewijzing verkrijgen we bij B-C-A en C-A-B
De drie andere toewijzingen leveren één correcte toewijzing : A-C-B B-A-C C-B-A
Merk op dat het dus onmogelijk is van precies twee correcte toewijzingen te hebben.
De getalwaarden van X zijn dus 0, 1, 2, 3 met als bijbehorende kans \(\frac26,\frac36,0,\frac16\)
De verwachtingswaarde is dus \(E(X)=0.\frac26+1.\frac36+2.0+3.\frac16=\frac36+\frac36=1\)

 Drie brieven zijn geadresseerd aan drie verschillende personen : Arne, Britt en Cathy.
Drie brieven zijn geadresseerd aan drie verschillende personen : Arne, Britt en Cathy. 