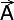 (x1,y1) en
(x1,y1) en 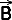 (x2,y2) twee plaatsvectoren/puntvectoren voorstellen
(x2,y2) twee plaatsvectoren/puntvectoren voorstellen(in een georthonomeerd assenstelsel), dan is de formule voor de afstand tussen A en B
Als 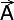 (x1,y1) en (x1,y1) en 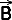 (x2,y2) twee plaatsvectoren/puntvectoren voorstellen (x2,y2) twee plaatsvectoren/puntvectoren voorstellen(in een georthonomeerd assenstelsel), dan is de formule voor de afstand tussen A en B |
A. \(\boldsymbol{\left|\,x_1. x_2+y_1. y_2\right|}\) |
|---|---|
| B. \(\large\boldsymbol{\left| \frac{y_2-y_1}{x_2-x_2}\right| }\) | |
| C. \(\boldsymbol{\sqrt{(x_2-x_1)^2\cdot (y_2-y_1)^2} }\) | |
| D. \(\boldsymbol{\sqrt{(x_1-y_2)^2+(x_2-y_1)^2} }\) | |
| E. \(\boldsymbol{\sqrt{(x_1-x_2)^2+ (y_1-y_2)^2} }\) |
[ 4,5-3540 - op net sinds 21.11.14-(E)-2.11.2023 ]
| IN CONSTRUCTION | A. |
|---|---|
| B. | |
| C. | |
| D. | |
| E. |
