|
|
|
|
10 |
\(\small \sqrt 8 + \sqrt{18}\) |
11 |
laatste cijfer kwadraat |
12 |
\(\small \sqrt 2 × \sqrt 2\) |
13 |
kwadraat van \(\frac{\sqrt{2}}{2}\) |
14 |
\(\small x.\sqrt x\) |
15 |
\(\small \sqrt x +\!\sqrt x = \sqrt x.\sqrt x\) |
16 |
\(2 < \sqrt 3 < 3\) |
17 |
vierkantswortel van 72 |
18 |
\(2\sqrt3 + 2\sqrt3\) |
19 |
\(\frac {1} {3}\;van\;\;?\;\;is\; \sqrt3 \) |
20 |
\(\sqrt 2 : (-\frac{1}{\sqrt2})\) |
21 |
\(2.3.\sqrt2.\sqrt6 \) |
22 |
\((1\!+\!\sqrt2):(1\!-\!2)\) |
28 |
\(\frac{1}{\sqrt2}\!+\!\frac{1}{\sqrt2} \) JWO2022 |
24 |
kwadraat van x−4 |
25 |
pos. vierkantsw. van 45 |
26 |
{X kwadraat van Y |
27 |
benaderen wortelvorm |
28 |
\(\frac ac\!\!\cdot\!\!\frac bc\!=\! \frac {a.b}{c}|\small \frac ac\!+\! \frac bc\!=\! \frac {a+b}{c}|\small \frac ab\!=\!\frac{a^2}{b^2}\) |
30 |
\(\frac {\sqrt{21}\,+\,\sqrt6} {\sqrt3} \) |
31 |
\(\frac {4\,+\,\sqrt{32}} {8} \) |
32 |
\(\frac {2\,+\,2\sqrt5} {2} \) |
33 |
\(\frac {3\,+\,3\sqrt6} {3} \) |
34 |
\( \frac {6\,+\,\sqrt{20}} {2} \) |
35 |
\( \frac {x} {\sqrt x}+ \frac {\sqrt x}{x} \) |
36 |
\(\frac {x} {\sqrt x}+x \) |
37 |
\(\frac {-4\,-\,\sqrt{32}} {-4} \) |
38 |
\(\frac {\sqrt2} {2}+\sqrt2 \) |
39 |
\(\frac {\sqrt3} {3} + \frac {2} {\sqrt3} \) |
40 |
\(\sqrt{4^4} \) |
41 |
\(\sqrt{16^{16}} \) |
42 |
\(\sqrt{0,36^{\,3}} \) |
43 |
\(\sqrt{16^{36}} \) |
44 |
\(\sqrt{16+\sqrt{16}}\: \approx \) |
45 |
\((\sqrt2\!+\!\sqrt8)^2 \) |
46 |
\((x^2\!-\,9)^2 \) |
47 |
\( (\sqrt5 - 2)^2\) |
48 |
\((5x)^2+5x^2 \) |
49 |
\(3.(-1).(3\sqrt3)^2\) |
50 |
\(\sqrt2.\sqrt3.\sqrt8 \) |
51 |
\( \small 2\!+\!\sqrt2+\sqrt2\!+\sqrt2.\sqrt2\) |
52 |
\(\small \sqrt1.\sqrt2.\sqrt3.\sqrt4\) |
53 |
\(\frac{\sqrt2}{2}.\frac{\sqrt2}{2}+\frac{\sqrt2}{2}+\frac{\sqrt2}{2} \) |
54 |
\((6\sqrt3)^2 - (3\sqrt2)^2 \) |
55 |
\(3\sqrt{27}-2\sqrt{12}+2\sqrt{75}\) |
56 |
f o u t ? |
57 |
alle vijf juist ? |
58 |
2 delen door\(\sqrt2\) |
59 |
helft van kwadraat |
60 |
3 gelijkheden ?_1 |
61 |
3 gelijkheden ?_2 |
62 |
3 gelijkheden ?_3 |
63 |
\(\text{l a t e r} \) |
64 |
4 gelijkheden ?_1 \) |
65 |
4 gelijkheden ?_2 |
66 |
5 gelijkheden ?_1 |
67 |
5 gelijkheden ?_2 |
68 |
5 gelijkheden ?_3 |
69 |
5 gelijkheden ?_4 |
70 |
5 gelijkheden ?_5 |
71 |
\(\text{l a t e r } \) |
72 |
wortel schatten |
73 |
kan berekend worden ? |
74 |
kleinste getal zkn |
75 |
grootste getal zoeken |
76 |
\((2\sqrt{2a})^2\) |
77 |
\( \small \sqrt x+\!\sqrt x+\!\sqrt x=\sqrt x.\sqrt x.\sqrt x\) |
78 |
\(\sqrt a > a\;\;?\) |
79 |
\(\small \sqrt{5^5+5^5+5^5+5^5+5^5} \) |
80 |
\( (\sqrt{20}+\sqrt5) :\! \sqrt5 \) |
81 |
\(\sqrt[3]{27}+\sqrt{36+64}+\sqrt{36.64} \) |
82 |
\(\ a^2 = -3 \Rightarrow \;? \) |
83 |
(88+88)+(88−88)+(88.88)+(88:88) |
84 |
helft van\(\sqrt{32} |
85 |
helft van een vierkantsw. |
86 |
vierkantsw. geh. getal |
87 |
\(\sqrt{2^2.6}-\sqrt{16}-\sqrt6\) |
88 |
\(\text{l a t e r }\) |
89 |
\( (x-\!1)^2\,+\,..?..\,= (x + 1 )^2 \) |
90 |
\( \sqrt{a^2.b^2}\) |
91 |
\(\small (1+3\sqrt2)^2-(1-3\sqrt2)^2\) |
92 |
\(\sqrt{(-x)^2}\) |
93 |
\(\small (\sqrt{10+\sqrt{75}} - \sqrt{10+\sqrt{75}})^2 \) |
94 |
\(\ \sqrt 5 \:\; \nabla \:\,\sqrt 5 \) |
95 |
\(\sqrt{36+64}+\!\sqrt{36.64}+\sqrt{36}+\!\sqrt{64}\) |
96 |
\((3+2\sqrt2)^2 \) |
97 |
\((\sqrt3+1)^4+(\sqrt3-1)^4 \) |
98 |
\((2\sqrt3 -5)^2\) |
99 |
\(\sqrt{3\!+\!\sqrt5}.\sqrt{3\!-\!\sqrt5} \) |
A0 |
\(\sqrt{6-4\sqrt2}\) |
A1 |
\(\frac {1} {2\,+\,\sqrt{3}} + \frac {2} {\sqrt{3}\,-\,1}\) |
A2 |
\(\sqrt{6+4\sqrt2}\) |
A3 |
\(\frac {1} {1-\sqrt{2022}} + \frac {1} {1+\sqrt{2022}}\)(J) |
A4 |
\((2\sqrt2+\sqrt3)^2\) |
A5 |
\(\bigl[4+\!\sqrt7)-(4\!-\!\sqrt7\bigr]^2 \) |
A6 |
\(3\,(2\sqrt3\,.\,4\sqrt5)\) |
A7 |
\(2 < \sqrt x < 3 \;\; en \;\; 1 < \sqrt x < 2 \) |
A8 |
\(\sqrt[4]{1 miljoen} \) |
A9 |
\(\small \sqrt6+\!2\leftrightarrow 2\sqrt2+\!\sqrt3\leftrightarrow \sqrt7\!+\!2\) |
B0 |
\(\sqrt5 + \sqrt{45}=\sqrt n \) |
B1 |
\(\scriptsize \sqrt{ 3^{n-4}\!+3^{n-3}\!+3^{n-2}\!+3^{n-1}\!+3^n}=33\) |
B2 |
30 keer 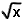 |
B3 |
meerdere vierkantswortels |
B4 |
\(\large \frac {\sqrt2} {\frac32}-\frac{\frac{\sqrt2}{3}}{2} \) |
B5 |
\(\frac 1x + x = 3\\\frac{1}{x^2}+x^2 =\;? \) |
B6 |
\((x - \frac 1x)^2 \) |
B7 |
\(2.(\,3.\sqrt{18}\,)(\,2.\sqrt3\,) \) |
B8 |
\(\sqrt{4-\sqrt{12}}\)  |
B9 |
\(\scriptsize\sqrt n+\!\sqrt n +\! \sqrt n =\sqrt n.\sqrt n.\sqrt n\)  |
C0 |
\(\large\frac{\sqrt{10}\,-\,\sqrt5}{\sqrt{10}\,+\,\sqrt5}\) 
|
C1 | \(\small\sqrt{e^2\!-\!6e\!+\!9}+\sqrt{e^2\!+\!6e\!+\!9}\)  |