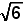
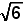
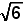
Driehoek ABC met  ∠C = 60° heeft een omgeschreven cirkel met straal 2.   Het punt D is een punt op het verlengde van [AC] zodanig dat   ∠ADB = 45°. Hoe groot is de straal van de omgeschreven cirkel van ΔABD ?	A.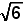
	B.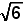
	C.   2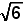
	D.
	E.    3

                     

[ vwo33-(1s29) - op net sinds 9.2.2018-()-8.9.2023 ]

Deze vraag werd gesteld op 17 januari 2018 tijdens de eerste ronde van de 33^ste Wiskunde Olypiade (5^de en 6^de jaars)
Slechts 8,5% van de deelnemers hadden het bij het juiste eind - 37% waren fout - 55% hebben niet geantwoord
Dit maakt dat deze vraag bij de top 3 zit van de meest moeilijke vragen van deze ronde.

Translation in   E N G L I S H

IN CONSTRUCTION The radius of the circumscribed circle (or: circumcircle) of ΔABC is 2. What is the radius of the circumscribed circle of ΔADB ?	A.   ½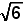
	B.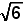
	C.   2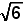
	D.
	E.    3

Oplossing - Solution

\(\text{Volgens de sinusregel in ΔABC is}\frac {|AB|} {\sin60 ^\circ }=2.2 \Leftrightarrow |AB|=4.\frac{\sqrt3}{2}=2\sqrt3 \)
Nu kunnen we ook de sinusregel toepassen in ΔABD (met x als straal omcirkel):