getallen x geldt dat
gelijk is aan
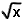
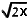
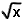
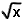
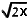
|
Voor alle positieve getallen x geldt dat gelijk is aan |
A. 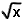 |
|---|---|
B. 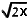 | |
C. 2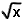 | |
D. 4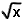 | |
E. 2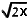 |
vwo33-(1j29) - op net sinds 9.2.2018-(E)-20.5.2022
Deze vraag werd gesteld op 17 januari 2018 tijdens de eerste ronde van de 17de Junior Wiskunde Olypiade (3de en 4de jaars)
14% juiste antwoorden - 44% foute antwoorden - 43% blanco's
Deze vraag mag bij de vijf moeilijkste gerekend worden.
|
For all positive numbers is equal to |
A. 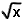 |
|---|---|
B. 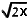 | |
C. 2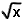 | |
D. 4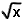 | |
E. 2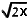 |
