2 3 b1 b2 gricha - vvwo32-(1s23) - 14.7.2022
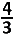
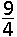
Een cirkel met straal 1 heeft koorden met lengte en .
De bijbehorende bogen hebben lengte b1 en b2.
Wat is de verhouding \(\small\boldsymbol{\frac {b_2} {b_1} ?}\)
A.  
B.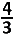  
C.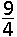  
D.   \(\boldsymbol{\sqrt {1,5}}\)
E.  
    a    b    c    d    e

vwo32-(1s23) - op net sinds 10.2.2017-()-9.12.2023 ]

Deze vraag werd gesteld op 18 januari 2017 tijdens de eerste ronde van de 16de Junior Wiskunde Olympiade en
de 32ste Wiskunde Olympiade, dus aan circa 25 000 leerlingen van het 3de, 4de, 5de en6de jaar
Deze vraag bleek de 'MOEILIJKSTE' van allemaal want ze haalde maar een scoringspercentage van 13%. Geen enkele andere vraag deed slechter !
42% heeft de vraag fout beantwoord en 45% lieten de vraag open. Uiteraard kon je verwachten dat D het topantwoord zou zijn (18%) maar ook A scoorde hoog (14%)

Translation in   E N G L I S H

IN CONSTRUCTION
A.  
B.  
C.  
D.  
E.  

Oplossing - Solution

Trek de loodlijn vanuit het middelpunt op de beide koorden zodat samen met de straat een rechthoekige driehoek ontstaat. De middelpuntshoek die op die koorde staat is evenredig met de lengte van de boog.
Voor b2 is die miidelpuntshoek α = 90° want \(\sin\frac{\alpha}{2}=\frac{\frac{\sqrt2}{2}}{1}\;\Rightarrow\;\frac{\alpha}{2}=45^\circ \)
Voor b1 is die miidelpuntshoek β = 120° want \(\sin\frac{\beta}{2}=\frac{\frac{\sqrt3}{2}}{1}\;\Rightarrow\;\frac{\beta}{2}=60^\circ \)
De booglengtes zijn evenredig met de middelpuntshoek zodat het antwoord is \(\frac{120^\circ}{90^\circ}=\frac43 \)
GWB