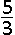
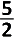
De figuur, bestaande uit één grote cirkel en vijf congruente kleinere cirkels, heeft vier symmetrieassen. We beschouwen twee gebieden: het rood gekleurde gebied (rechts) en de twee blauwe cirkels. De verhouding van de oppervlakte van het grootste gebied tot dat van het kleinste gebied is	A.   1
	B.
	C.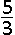
	D.   2
	E.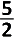

                     

[ vwo27-(1j27) - op net sinds 8.11.2022-(E)-18.11.2023 ]

Deze (27^ste) vraag werd gesteld in januari 2012 tijdens de eerste ronde van de 11^de Junior Wiskunde Olypiade (3^de en 4^de jaar)
21,5% van de deelnemers gaven een juist antwoord. Meer dan een derde liet de vraag blank.
De vraag behoort tot de vijf moeilijkste vragen (van de 30 gestelde)

Translation in   E N G L I S H

IN CONSTRUCTION	A.
	B.
	C.
	D.
	E.

Oplossing - Solution

Als de straal van de kleine cirkels R is, is de straal van de grote cirkel 3R.
De oppervlakte van de twee kleine cirkels is 2πR².
De oppervlakte van het rode gebied is \(\boldsymbol{\frac {\pi (3R)^2 - 5\pi R^2} {4} = \frac{4\pi R^2}4 = \pi R^2 }\)
De gevraagde verhouding is dus 2.