.png)
Een bol past precies in een cilinder (zie figuur). Als
men het middelpunt van het bovenvlak verbindt met
de twee eindpunten van een middellijn van het grondvlak
ontstaat er een hoek a. Hoe groot is cos α ?
| A. 0,4 |
|---|---|
| B. 0,5 | |
| C. 0,6 | |
D.  | |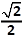
| E. 0,8 |
Deze (28ste) vraag werd gesteld op 17 januari 207 tijdens de eerste ronde van de 22ste Wiskunde Olypiade (5de en 6sup>de jaar)
Slechts 11,5% van de deelnemers gaven een juist antwoord, 44% foute antwoorden en 44% blanco's.
Alternatief B en alternatief D scoorden hoger dan het juiste antwoord !
|
IN CONSTRUCTION |
A. |
| B. | |
| C. | |
| D. | |
| E. |
De basis van de driehoek is 2R (dubbel van de straal van de bol).
De opstaande zijden vindt men door een hoogtelijn in deze gelijkbenige driehoek te tekenen en de stelling van Pythagoras toe te passen :
^2}=\sqrt{5R^2}=\sqrt&space;5\,R "https://latex.codecogs.com/png.image?\dpi{110}\sqrt{R^2+(2R)^2}=\sqrt{5R^2}=\sqrt 5\,R")
In de gelijkbenige driehoek kan men nu de cosinusregel toepassen op de basis :
(2R)² = 5R² + 5R² − 2
R.R.cos α
⇔ 4R² = 10R² − 10R².cos α
⇔ 10R².cos α = 6R²
⇔ cos α = 0,6
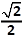
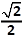
In de gelijkbenige driehoek kan men nu de cosinusregel toepassen op de basis :
(2R)² = 5R² + 5R² − 2
R.R.cos α⇔ 4R² = 10R² − 10R².cos α
⇔ 10R².cos α = 6R²
⇔ cos α = 0,6