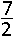
Een halve cirkel met straal 1 verdeelt men in een boog van 45° en een boog van 135°. Het verdeelpunt en de eindpunten van de middellijn bepalen een driehoek. Wat is de som van de oppervlakten van de gelijkzijdige driehoeken (zie grijze arcering) die elk een zijde met de driehoek gemeen hebben?	A.
	B.   π
	C.   3
	D.   2
	E.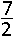

                     

[ vwo22-(1s20) - op net sinds .11.2022-(E)-27.12.2023 ]

Deze (20^ste) vraag werd gesteld op 17 januari 2007 tijdens de eerste ronde van de 22^ste Wiskunde Olypiade (5^de en 6^de jaar)
slechts 17% van de deelnemers gaf een correct antwoord.
Deze vraag had het hoogste aantal blanco's : 60%

Translation in   E N G L I S H

Oplossing - Solution

Weze a,b,c de lengtes van de zijden van de driehoek (a schuine zijde).
Met de formule ½ a.b.sinC voor de oppervlakte van een driehoek verkrijgt men voor de totale oppervlakte :
½ a².sin 60° + ½ b².sin 60° + ½ c².sin 60° = ½ sin 60°(a² + b² + c²)
= ½ sin 60°.2a² = a².sin 60° = 2². = 2