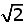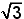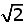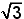|
In een driehoek met hoeken 30°, 60° en 90° trekt men de bissectrice uit de hoek van 60°. Hierdoor wordt de driehoek verdeeld in twee driehoeken waarvan de verhouding van de oppervlakten gelijk is aan
|
A. 1 |
|---|
| B. 1,5 |
C. 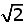 |
D. 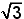 |
| E. 2 |
| F. 2,5 |
[ 3-8895 - op net sinds 23.5.2024-(E)- ]
Translation in E N G L I S H
Oplossing - Solution
In zo'n driehoek is de lengte van de schuine zijde precies het dubbel van de kleinste rechthoekszijde (een gevolg van het feit dat sin 30° = ½)
De bissectricestelling zegt dat andere rechthoekszijde precies verdeeld wordt in de verhouding van de twee andere zijden. Het ene stuk is dus dubbel zo lang als het andere. En vermits de oppervlakte van twee driehoeken die dezelfde hoogte hebben zich verhouden als de lengte van hun basissen is, het antwoord dus 2.