Wiskunde Multiple Choice Vraag

Een regelmatig viervlak is een viervlak waarbij alle ribben even lang zijn (hier 2). Tevens is dat viervlak een regelmatige piramide. Hoe groot is de cosinus van de hoek die elke twee zijvlakken met elkaar maken ?	A. $\frac35$
B. $\frac12$
C. $\frac13$
D. $\frac{\sqrt3}{3}$
E. $\frac{\sqrt5}{5}$
F. 0

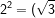De driehoek die de twee gestippelde lijnen bevat is niet een rechthoekige driehoek maar een gelijkbenige driehoek met opstaande zijde $\sqrt{2^1-1^2}=\sqrt3$ (Pythagoras). De basis van deze gelijkbenige driehoek is een ribbe van het viervlak (lengte 2). Door de cosinusregel toe te passen op deze zijde (die tegenover de gevraagde hoek ligt), vindt men $2^2=(\sqrt3)^2+(\sqrt3)^2-2.(\sqrt3)^2.(\sqrt3)^2.\cos x\;\Leftrightarrow\:2.3\cos x=3+3-4\\\;\Leftrightarrow\:6.\cos x=2\;\Leftrightarrow\:\cos x=\frac13$
(x = 70°31′44″)