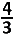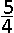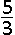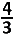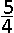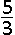1ste manier :
Noem α de twee delen van de hoek in B.
Dan is \(\tan \alpha =\frac12\) en \(\tan 2\alpha=\frac{x+1}{2}\).
Met de verdubbelingsformule voor tan 2α verkrijgen we een vergelijking in x
waaruit de waarde van x zal volgen :
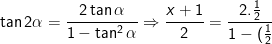^2}\\\Leftrightarrow\;\frac{x+1}{2}=\frac{1}{\frac34} "\\\tan2\alpha=\frac{2\tan\alpha}{1-\tan^2\alpha}\\\Rightarrow\frac{x+1}{2}=\frac{2.\frac12}{1-(\frac12)^2}\\\Leftrightarrow\;\frac{x+1}{2}=\frac{1}{\frac34}")
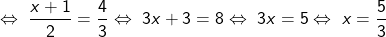2de manier :
De schuine zijde van de rechthoekige driehoek ABC heeft de lengte \(\sqrt{4+(1+x)^2} \) (Pythagoras).
Wegens de bissectricestelling in en driehoek is
\(\frac21 = \frac {\sqrt{4+(1+x)^2}} {x}\)
⇔ 2x = \(\sqrt{4+(1+x)^2}\)
⇒ 4x² = 4 + 1 + 2x + x²
3x² − 2x − 5 = 0
Deze vierkantsvergelijking heeft als discriminant
D = 4 + 60 = 64 zodat \(\large x_{1,2}=\frac {2\pm 8}6\)
Enkel de positieve oplossinhg \(\frac {2+8} {6}=\frac53 \) kan weerhouden worden en is dus ook het antwoord.
