Het is bekend dat voor het getal e geldt :

Waaraan is dan de volgende som gelijk ?
)
Waaraan is dan de volgende som gelijk ?
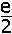
|
Het is bekend dat voor het getal e geldt : Waaraan is dan de volgende som gelijk ? |
A. e + 2 |
|---|---|
| B. e2 | |
| C. 2e2 | |
| D. 2e | |
E. 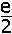 | |
| F. e + 1 |
[ 6-8768 - op net sinds 22.3.2023-()-3.11.2024 ]
|
IN CONSTRUCTION |
