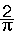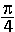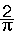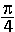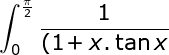^2}\;&space;dx\;=)
Moeilijke bepaalde integraal
|
A. 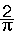 |
|---|
B. 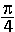 |
C.  |
| D. π |
| E. 2π |
[ 6-8752 - op net sinds 13.11.2022-(E)-2.11.2023 ]
Translation in E N G L I S H
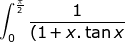^2}\;&space;dx\;=)
|
A. |
|---|
| B. |
| C. |
| D. |
| E. |
Oplossing - Solution
\(
INT = \int_{0}^{\frac{\pi}{2}}\frac{1}{(1\!+x.\tan x)^2}\: dx=
\int_{0}^{\frac{\pi}{2}}\frac{\cot^2x} {(\cot x + x)^2}\: dx\\
Stel \; \cot x + x = y\\
\scriptsize \quad (x\to 0\;\;k.o.m.\;y\to +\infty \quad x\to \frac{\pi}{2}\;k.o.m.\;y=\frac{\pi}{2})\\
\Rightarrow \left( - \; \frac {1}{\sin^2 x} + 1 \right) dx=dy\\
\Rightarrow \frac {\sin^2x\,-\: 1}{\sin^2x }dx=dy\\
\Rightarrow \cot^2x\;dx = -\:dy\\
INT= \int_{+\infty}^{\frac{\pi}{2}} \left( -\;\frac{1}{y^2}\right) \; dy=\left [ \frac 1y \right ]_{+\infty}^{\frac{\pi}{2}}=\frac{1}{\frac{\pi}{2}}=\frac{2}{\pi}\approx 0,63662
\)