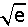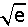\(\int_{0}^{1}\frac{1}{\sqrt{-ln}}\;\ dx=\)
Stel \(t=\sqrt{-ln\ x}\Leftrightarrow\; -t^2==ln x \;\Leftrightarrow\; x=e^{-t^2}\)
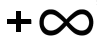
x = 0  en  x = 1  corresponderen dan met  en 0   dx = −2 t e^−t²dt
\(\int_{0}^{1}{\frac{1}{\sqrt{-\ln x}}}\;dx=\int_{+\infty}^0\frac{-2te^{-t^2}}{t}dt=2\int_0^{+\infty} e^{-t^2} dt=\int_{-\infty}^{+\infty}e^{-t^2}\;dt\) (even functie)
Dit is de Gaussiaanse integraal, dus gelijk aan \(\sqrt\pi\)
Toelichting : voor de normale distributie  N(μ,σ)  is
\(\int_{-\infty}^{+\infty}{\frac{1}{\sigma\sqrt{2\pi}}}\ e^{-\frac{(x-\mu)^2}{2\sigma^2}}dx=1 \)
Voor \(\mu=1\)  μ = 1  en  \(\sigma=\frac{1}{\sqrt2}\) verkrijg je de Gaussiaanse integraal :
\(\int_{-\infty}^{+\infty}\frac{\sqrt2}{\sqrt{2\pi}}e^{-x^2}dx=1\;\Rightarrow\;\int_{-\infty}^{+\infty}e^{-x^2}dx=\sqrt\pi\)