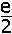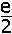^{\frac&space;1x}\,-\,e}&space;{x}&space;=)
|
A. 0 |
|---|
| B. 1 |
| C. e |
| D. − e |
E. − 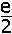 |
[ 6-8727 - op net sinds 5.4.2021-(E)-6.11.2024 ]
Translation in E N G L I S H
Oplossing - Solution
\(\left [D\; x^x= D\; e^{\ln x^x} = e^{\ln x^x}\cdot D\;\ln x^x =x^x\cdot D(x.\ln x) \right ] \\ \lim_{x \to 0}\frac{(1+x)^\frac{1}{x}-e}{x}\left (=\frac{0}{0} \right )\begin{matrix} H\\ =\\ {\color{Yellow} .} \end{matrix} \; \lim_{x \to 0}\; D\: (1+x)^\frac{1}{x}\\ =\lim_{x \to 0}\; D\: e^{\frac{\ln (1+x)}{x}} =\lim_{x \to 0}\;\left [e^{\frac{\ln (1+x)}{x}}\cdot \frac{\frac{1}{1+x}.x-\ln(1+x)}{x^2} \right ]\\ =\lim_{x \to 0}\;e^{\frac{\ln (1+x)}{x}}\cdot \lim_{x \to 0}\frac{\frac{1+x-x}{(1+x)^2}-\frac{1}{1+x}}{2x} \quad ^{{\color{DarkRed} (with\; de\; l'Hospital)}} \\ =e\: \cdot \lim_{x \to 0}\;\frac{\frac{1-1-x}{(1+x)^2}}{2x} =e\: \cdot \lim_{x \to 0}\;\left ( -\frac{1}{2(1+x)^2} \right )=e\left ( -\frac{1}{2} \right )=-\frac{e}{2}\)