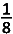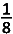\(\\ {\color{DarkGreen} 1^{ste} manier :}\\ \displaystyle\lim_{x \to -2}\frac{\sqrt{1+\sqrt{x+6}}-\sqrt{3}}{x+2}\left (=\frac{0}{0} \right ) \\ = \displaystyle\lim_{x \to -2}\frac{1+\sqrt{x+6}-3}{(x+2)(\sqrt{1+\sqrt{x+6}}+\sqrt{3})} \\ =\displaystyle\lim_{x \to -2}\frac{(\sqrt{x+6}-2)(\sqrt{x+6}+2)}{(x+2)(\sqrt{1+\sqrt{x+6}}+\sqrt{3}) ((\sqrt{x+6} +2) } \\ =\displaystyle\lim_{x \to -2}\frac{x+6-4}{(x+2)(\sqrt{1+\sqrt{x+6}}+\sqrt{3}) (\sqrt{x+6} +2) } \\ =\displaystyle\lim_{x \to -2}\frac{1}{(\sqrt{1+\sqrt{x+6}}+\sqrt{3}) (\sqrt{x+6} +2) } \\ =\frac{1}{(\sqrt{1+2}+\sqrt{3(2+2})}=\frac{1}{2\sqrt{3}.4}=\frac{1}{8\sqrt{3}}=\frac{\sqrt{3}}{24} \\ {\color{DarkGreen} 2^{de} manier :}\\ \displaystyle\lim_{x \to -2}\frac{\sqrt{1+\sqrt{x+6}}-\sqrt{3}}{x+2}\left (=\frac{0}{0} \right ) \\ \begin{matrix} H\\ = \end{matrix} \displaystyle\lim_{x \to -2}\frac{1}{2\sqrt{1+\sqrt{x+6}}}\cdot \frac{1}{2\sqrt{x+6}}=\frac{1}{8\sqrt{3}}=\frac{\sqrt{3}}{24}\)