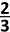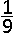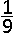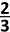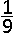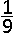}&space;{\ln(1\,+\,3x^4\,+\,9x^8)})
is gelijk aan
|
A. 1 |
|---|
B.  |
C. 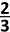 |
D. 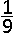 |
E. − 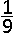 |
[ 6-8711 - op net sinds 2.4.2021-(E)-28.8.2025 ]
Translation in E N G L I S H
Oplossing - Solution
\( \displaystyle\lim_{x\rightarrow +\infty }\: \frac{\ln\, (1+2x^2+4x^4)}{\ln\, (1+3x^4+9x^8)}\left ( =\frac{+ \infty}{+ \infty} \right ) \\ \begin{matrix} H\\ =\\ \end{matrix} \displaystyle\lim_{x\rightarrow +\infty }\:\frac{\frac{1}{1+2x^2+4x^4}\cdot D(1+2x^2+4x^4) }{\frac{1}{1+3x^4+9x^8}\cdot D(1+3x^4+9x^8)} \\ =\displaystyle\lim_{x\rightarrow +\infty }\:\left [ \frac{4x^2+16x^3}{1+2x^2+4x^4} \cdot \frac{1+3x^4+9x^8}{12x^3+72x^7} \right ] \\ =\displaystyle\lim_{x\rightarrow +\infty }\:\: \frac{16\cdot 9\cdot x^{11}+...lagere \; graadstermen}{4\cdot 72\cdot x^{11}+...lagere \; graadstermen} \\ =\displaystyle\lim_{x\rightarrow +\infty }\:\: \frac{16\cdot 9}{4\cdot 72}=\frac{4}{8}=\frac{1}{2}\)