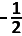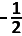}&space;{\log_4\,&space;(\cos&space;x)}&space;=)
|
A. 1 |
|---|
| B. 2 |
| C. 4 |
| D. − 2 |
| E. − 4 |
F. 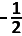 |
[ 6-8704 - op net sinds 3.5.2021-(E)-6.11.2024 ]
Translation in E N G L I S H
Oplossing - Solution
\(\displaystyle\lim_{{x\to 0}}\;\frac{\log_2\,(1-x^2)}{\log_4\,(\cos x)}\left(=\frac00\right)\overset{H}{=}\displaystyle\lim_{{x\to 0}}\;\frac{\frac{1.(-2x)}{(1-x^2).\ln2}}{\frac{1.(-\sin x)}{\cos x.\ln4}}=\displaystyle\lim_{{x\to 0}}\;\frac{2x.\cos x.\ln2^2}{(1-x^2).\ln2.\sin x}\\=\displaystyle\lim_{{x\to 0}}\;\frac{2(\cos x).2.\ln2}{(1-x^2).\ln2}.\displaystyle\lim_{{x\to 0}}\;\frac{x}{\sin x}=\frac{2.1.2}{1}.1=4\)