1^ste manier : algebraïsch
Via substitutie verkrijgen we de volgende vierkantsvergelijking :
x² + (r − x)² = r x² + r² −2rx + x² − r = 0 2x² − 2rx + r² − r = 0
De rechte x + y = r en de cirkel x² + y² = r zullen dus minstens één snijpunt hebben als de discriminant minstens nul is.
D = 4r² − 8(r² − r) = 4r² − 8r² + 8r = 8r − 4r² = 4r(2 − r)
Voor r tussen 0 en 2 zullen er twee oplossingen zijn.
Voor r = 0 of r = 2 is er één oplossing.
Het antwoord is dus [0,2]
2^de manier : meetkundig
r moet minstens 0 zijn anders is de cirkel   x² + y² = r
geen reële cirkel (met straal √r en middelpunt O)
x + y = r   ⇔   y = − x + r
stelt een rechte voor evenwijdig aan de tweede bissectrice en die van het eerste kwadrant een gelijkbenige rechthoekige driehoek afsnijdt met rechthoekszijden  r  en schuine zijde  r.
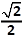
De hoogte h (vanuit O) van die driehoek is dus gelijk aan   h =  r
Opdat de cirkel (met straal √r) minstens één snijpunt zou hebben met de rechte moet
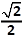
.r ≤ √r ⇔ r ≤ 2.√r ⇔ 2r² ≤ 4r ⇔ 2r(r − 2) ≤ 0 ⇔ r ∈ [ 0, 2 ]