De afstand van het punt (2,0) tot een punt van de parabool/kromme y = 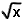 is het kleinst voor x gelijk aan
is het kleinst voor x gelijk aan
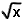 is het kleinst voor x gelijk aan
is het kleinst voor x gelijk aan



|
De afstand van het punt (2,0) tot een punt van de parabool/kromme y =
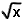 is het kleinst voor x gelijk aan is het kleinst voor x gelijk aan
|
A. 1 |
|---|---|
B.  | |
C.  | |
D.  | |
| E. 2 |
[ 4-8659 - op net sinds 6.4.2021-(E)-4.11.2023 ]
|
IN CONSTRUCTION |
|---|
