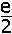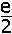1ste manier :
Snijpunt van y = 2 met y = ex heeft als abscis de oplossing van 2 = e
x, m.a.w. x = ln 2.
De gevraagde oppervlakte S is bijgevolg de oppervlakte van een rechthoek, nl. 2.ln 2 verminderd met de bepaalde integraal :
=2.\ln&space;2&space;-&space;1&space;\approx&space;0,3863 "S=2.\ln 2 - \int_{0}^{\ln 2}e^x dx \newline {\color{Green} .}\quad \; = 2\cdot \ln 2 -\left [ e^x \right ]{_{0}^{\ln 2}}=2.\ln 2- (2\!-\! 1)=2.\ln 2 - 1 \approx 0,3863")
2de manier :
Spiegel de kromme t.o.v. de rechte y = 1. De nieuwe vergelijking wordt dan y = − e
x + 2 die de x-as snijdt in ln 2.
De gevraagde oppervlakte is precies dezelfde als de oppervlakte begrensd door die kromme, de x-as en de rechte x = ln 2. Bijgevolg
dx&space;=&space;\left&space;[&space;-e^x\!+\!2x\right&space;]{_{0}^{\ln&space;2}}=-2&space;+&space;2.\ln&space;2&space;+&space;1&space;=&space;2.\ln&space;2\!-\&space;1 "S=\!\int_{0}^{\ln 2}(-e^x+2)dx = \left [ -e^x\!+\!2x\right ]{_{0}^{\ln 2}}=-2 + 2.\ln 2 + 1 = 2.\ln 2\!-\ 1")
