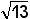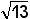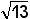|
Hoe groot is de straal van de om-geschreven cirkel van de driehoek OAB waarbij A(6,0) en B(0,4) twee hoekpunten zijn ?
|
A. 4 |
|---|
| B. 5 |
| C. 6 |
| D. 10 |
E. 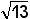 |
[ 4-8519 - op net sinds 29.6.2020-(E)-22.10.2023 ]
Translation in E N G L I S H
|
What is the radius of the circumscribed circle of the triangle OAB where A(6,0) and B(0,4) are two vertices?
|
A. 4 |
|---|
| B. 5 |
| C. 6 |
| D. 10 |
E. 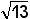 |
Oplossing - Solution
Middelpunt van de cirkel ligt in het midden van de schuine zijde van de driehoek, dus in het punt dat het midden is van [AB], nl. M(3,2).
De straal van de cirkel is dan de afstand van dat punt tot de oorsprong, dus √3² + 2² = √13.
Dit is dezelfde afstand als van A(6,0) tot M(3,2) !
Dit is ook dezelfde afstand als van B(0,4) tot M(3,2) !