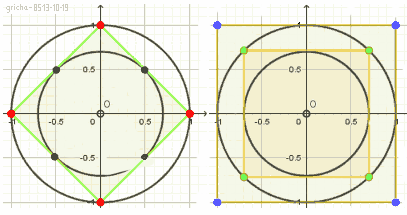
Alle vierdemachtswortels uit − 1 worden in het vlak van GAUSS weergegeven door
 Alle vierdemachtswortels uit − 1 worden in het vlak van GAUSS weergegeven door |
A. de rode punten (links) |
|---|---|
| B. de zwarte punten (links) | |
| C. de blauwe punten (rechts) | |
| D. de groene punten (rechts) | |
| E. een combinatie van twee kleuren |
[ 5-8513 - op net sinds 18.7.2020-(E)-3.5.2025 ]
|
fourth roots of −1 IN CONSTRUCTION |
A. red dots |
|---|---|
| B. black dots | |
| C. blue dots | |
| D. green dots | |
| E. a combination |
