Wat is de
modulus van

|
A. 1 |
|---|
B.  |
C.  π π |
| D. 0 |
| E. 75 |
[ 6-8500 - op net sinds 9.9.2019-(E)-4.2.2024 ]
Translation in E N G L I S H
Wht is the
modulus of
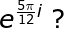
|
A. 1 |
|---|
B.  |
C.  π π |
| D. 0 |
| E. 75 |
Oplossing - Solution
Alle complexe getallen van de vorm \(e^{ix}\) liggen (in het vlak van GAUSS)
op een cirkel met straal 1 (en met argument x).
Hun modulus is dus 1 (afstand tot de oorsprong)
Vandaar dat ook \(e^\frac{5\pi}{12}i\) modulus 1 heeft.
Overigens is \(e^\frac{5\pi}{12}=\cos\frac{5\pi}{12} +i.\sin\frac{5\pi}{12} =\cos 75 ^\circ + i.\sin75 ^\circ \)
en kan elk complex getal z op drie manieren geschreven worden :
a + bi of
r.(cos α + i sin α) afgekort r.cis α of
r.eα i



 π
π
 π
π