f (x + p) = f (x) , en dit voor elke (reële) x-waarde.
Wat is de periode van de functie
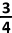 p
p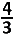 p
p (3p + 5)
(3p + 5)|
De periode van de functie f is p, d.w.z. dat p het kleinste strikt positieve getal is waarvoor f (x + p) = f (x) , en dit voor elke (reële) x-waarde. Wat is de periode van de functie |
A. 3p |
|---|---|
| B. 4p | |
C. 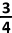 p p | |
D. 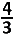 p p | |
E.  (3p + 5) (3p + 5) |
[ 5-8467 - op net sinds 23.10.2020-(E)-15.12.2023 ]
|
IN CONSTRUCTION |
|---|
