Vind je een fout in de opgave, zelfs een spellingsfout of een layout die beter kan of een figuur die niet doorkomt, of een verkeerde vraag bij een opgave : gelieve mij een lege mail te sturen ( gricha@gricha.be ) met alleen in het onderwerp bv. vraag 9876 nakijken a.u.b. Bedankt !
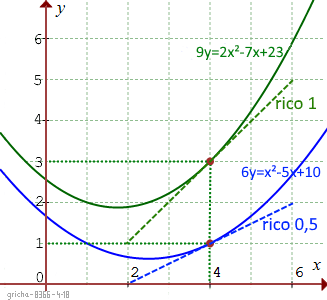
In de figuur zie je de grafieken van
1) de functie f , een parabool met vgl.
6y = x² − 5x + 10 gaande door (4,1);
in dat punt heeft de raaklijn rico 0,5
2) de functie g, een parabool met vgl.
9y = 2x² − 7x + 23 gaande door (4,3);
in dat punt heeft de raaklijn rico 1
Wat is de richtingscoëfficiënt (rico) van de raaklijn van het product van de functies f en g (f.g) in het punt met abscis 4 ?
|
A. 0,5 |
|---|
| B. 1 |
| C. 1,5 |
| D. 2 |
| E. 2,5 |
[ 5-8366 - op net sinds 11.6.2020-(E)-14.11.2024 ]
Translation in E N G L I S H
Oplossing - Solution
1ste manier : (meest aangewezen manier)
De richtingscoëfficiënt van de raaklijn van de functie f.g in het punt met abscis 4
is de getalwaarde voor 4 van de afgeleide van de functie f.g.
[ (f.g) ′ ]x=4 = [ f ′. g + f.g ′ ]x=4 = (0,5).3 + 1.(1) = 1,5 + 1 = 2,5
2de manier : (niet aangewezen manier; 54 om breuken te vermijden)
54.h(x) = 54. f(x).g(x) = (x² − 5x + 10 ).(2x² − 7x + 23)
= (2x4 − 7x³ + 23x² − 10x³ + 35x² − 115x + 20x² − 70x + 230)
= (2x4 − 17x³ + 78x² − 185x + 230)
54.h ′(x) = 8x³ − 51x² + 156x − 185
Dus 54.h ′(4) = 8.64 − 51.16 + 156.4 − 185 = 512 − 816 + 624 − 185 = 135
h ′(4) = 135 : 54 = 2,5