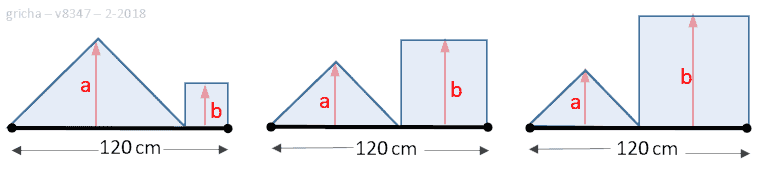
Op een lijnstuk van 120 cm tekent men een rechthoekige gelijkbenige driehoek en een vierkant op een manier zoals de drie figuren laten zien.
Wat is de zijde van het vierkant dat ervoor zorgt dat de som van de kwadraten van de afstanden a (hoogte driehoek) en b (zijde vierkant) zo klein mogelijk is ?
|
A. 20 |
|---|
| B. 24 |
| C. 25 |
| D. 30 |
| E. 48 |
[ 4-8347 - op net sinds 23.10.2020-(E)-23.10.2023 ]
Translation in E N G L I S H
a2 + b2 minimum
for what side of square ?
|
A. 20 |
|---|
| B. 24 |
| C. 25 |
| D. 30 |
| E. 48 |
Oplossing - Solution
Noem x de lengte van de zijde van het vierkant (=b).
De schuine zijde van de driehoek is dan 120 − x en de hoogte (a) 60 − ½x.
Bijgevolg is de som S van de kwadraten van a en b gelijk aan
S = (60 − ½x)² + x² = 3600 − 60x + ¼x² + x² = 1,25x² − 60x + 3600
Dit is een kwadratische uitdrukking (dalparabool) met een
minimumwaarde voor x = 60 / 2,5 = 240 / 10 = 24


