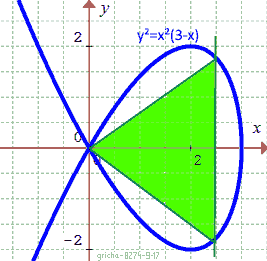
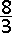De blauwe lijn geeft de grafiek weer van y² = x².(3 − x), een grafiek die lijkt op een gespiegelde letter alfa.
De rechte x = k ( 0 < k < 3) snijdt deze in twee punten die met de oorsprong een gelijkbenige driehoek vormen.
Voor welke waarde van k is die driehoek gelijkzijdig ?
|
A. 2 |
|---|
| B. 2,4 |
| C. 2,5 |
D.  |
E.  |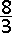
[ 6-8345 - op net sinds 9.2.2018-(E)-3.11.2023 ]
Translation in E N G L I S H
IN CONSTRUCTION
Graph : y² = x².(3 − x)
Line : x = k
equilateral triangle
for k = ?
|
A. 2 |
|---|
| B. 2,4 |
| C. 2,5 |
| D. |
| E. |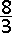
Oplossing - Solution
De rechte x = k snijdt de kromme in punten met ordinaat \(\boldsymbol{\scriptsize\pm \, k\sqrt{3-k}}\).
De verticale zijde van de driehoek heeft dus een lengte van \(\boldsymbol{\scriptsize 2k\sqrt{3-k}}\).
De andere zijde(n) hebben een lengte van \(\boldsymbol{\scriptsize\sqrt{k^2\!+k^2(3-k)}=k\sqrt{1+3-k}=k\sqrt{4-k} }\)
Opdat de driehoek gelijkzijdig zou zijn moet \(\boldsymbol{\scriptsize 2k\sqrt{3-k}=k\sqrt{4-k}\: \Leftrightarrow \: 4(3-k)=4-k\: \Leftrightarrow \: 12-4k=4-k\: \Leftrightarrow \:8=3k\: \Leftrightarrow \:k=\frac 83}\)
