Wiskunde Multiple Choice Vraag

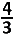
Een horizontale rechte y = k snijdt de rechte y = x in het punt A en de hyperbool x² − y² = 1 in het punt B. Voor welke (positieve) waarde van k is de afstand van A tot B het kleinst ?	A. 1
B. 1,5
C. 2
D.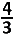
E.

IN CONS IN CONSTR IN CONSTRUC IN CONSTRUCTI IN CONSTRUCTION	A.
B.
C.
D.
E.

y = k snijdt de rechte y = v2puur

x in $\left(\frac{k}{\sqrt2},k\right)$ en de hyperbool x² − y² = 1 in punten die volgen uit de oplossing van $x^2-k^2=1\;\Leftrightarrow\;x^2=1+k^2\;\Leftrightarrow\;x=\pm\sqrt{1+k^2}$ .
In het eerste kwadrant is dit dus het punt $\left(\sqrt{1+k^2},k\right)$ .
Bijgevolg is |AB| = $\sqrt{1+k^2}-\frac k{\sqrt2}$ .
Om het minimum te vinden berekenen we de afgeleide naar k :
$\mathbf{D}_k\,|AB|=\mathbf{D}_k\,\left(\sqrt{1+k^2}-\frac k{\sqrt2}\right)=\frac{1.2k}{2\sqrt{1+k^2}}-\frac1{\sqrt2}=\frac{\sqrt2k-\sqrt{1+k^2}}{\sqrt2.\sqrt{1+k^2}}$
De nulwaarde van deze afgeleide volgt uit
$\\\sqrt2k-\sqrt{1+k^2}=0\;\Leftrightarrow\;\sqrt2\,k=\sqrt{1+k^2}\;\Rightarrow\;2k^2=1+k^2\;\Leftrightarrow\;k^2=1\;\Leftrightarrow\;k=\pm1$
Vermits k positief moet zijn en we wel degelijk een minimum verwachten kan dat alleen maar zijn voor k = 1.