Wat is het bereik
van de functie
=\sqrt{8x-x^2})
|
A. [ 0, 2 ] |
|---|
| B. [ 0, 4 ] |
| C. [ 0, 8 ] |
| D. [ 0, 16 ] |
E. [ 0, 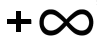 [ [ |
[ 4-8317 - op net sinds 28.3.2018-(E)-8.12.2024 ]
Translation in E N G L I S H
What is the range of the function
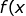=\sqrt{8x-x^2})
|
A. [ 0, 2 ] |
|---|
| B. [ 0, 4 ] |
| C. [ 0, 8 ] |
| D. [ 0, 16 ] |
| E. [ 0, ∞ ) |
Oplossing - Solution
1ste manier :
y = 8x − x² = x(8 − x) is het voorschrift van een bergparabool met top
\(T\left(\frac{0+8}{2},f(\frac{0+8}{2})\right)=T(4,f(4)) = T(4,16)\).
De bergparabool heeft dus punten met een positieve y-waarde van 0 t/m 16.
Het bereik van \(f(x)=\sqrt{8x-x^2}\) is dus [0,\(\sqrt{16}\)] = [ 0, 4 ]
2de manier :
\(y=f(x)=\sqrt{8x-x^2}\) is het voorschrift van een halve cirkel
met middelpunt M ( 4, 0 ) en straal 4 ! Dit kunnen we afleiden uit :
\(\small y=(x)=\sqrt{8x-x^2}\)
⇔ y² = 8x − x² ∧ y ≥ 0
⇔ x² − 8x + y² = 0 ∧ y ≥ 0
⇔ x² − 8x + 16 + y² = 16 ∧ y ≥ 0
⇔ (x − 4)² + y² = 16 ∧ y ≥ 0
Hieruit kunnen we ook besluiten dat het bereik [ 0, 4 ] is.
[ (x − a)² + (y − b)² = r² is de vergelijking van een cirkel met
middelpunt M ( a, b ) en straal r ]

=\sqrt{8x-x^2})
