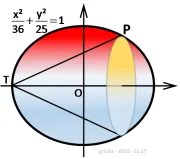
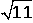 Een punt P(x,y) op de omtrek van de ellips met vergelijking \(\boldsymbol{\frac {x^2} {36} + \frac {y^2} {25} =1}\)
laat men wentelen rond de x-as zodat een cirkel ontstaat als grondvlak van een kegel met top T(− 6, 0).
Een punt P(x,y) op de omtrek van de ellips met vergelijking \(\boldsymbol{\frac {x^2} {36} + \frac {y^2} {25} =1}\)
laat men wentelen rond de x-as zodat een cirkel ontstaat als grondvlak van een kegel met top T(− 6, 0).
Wat moet de abscis van P zijn opdat de inhoud van de kegel zo groot mogelijk zou zijn ?
|
A. 0 |
|---|
| B. 1 |
| C. 2 |
| D. 3 |
E. 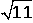
(plaats van het
brandpunt) |
[ 5-8316 - op net sinds 20.2.2022-(E)-22.6.2025 ]
Translation in E N G L I S H
Oplossing - Solution
\(\frac{x^2}{36}\!+\!\frac{y^2}{25}=1 \Leftrightarrow 25x^2\!+\!36y^2=36.25 \Leftrightarrow y^2=\frac{36.25-25x^2}{36} \Leftrightarrow y^2=\frac{25}{36}(36-x^2)\)
De straal van het grondvlak van de kegel is y of \(\frac56\sqrt{36-x^2}\).
De hoogte van de kegel is 6 + x.
Het volume V van de kegel is bijgevolg \(\frac13\pi\frac{25}{36}(36-x^2)(6+x)=\frac{\pi}{3}(-x^3-6x^2+36x+6^3)\)
De nulwaarden van de afgeleide van V gaan ons naar het antwoord leiden.
\(\small D\;V=\frac{25\pi}{108}.D\:(-x^3\!-\!6x^2\!+\!36x\!+\!6^3)=\frac{25\pi}{108}(-3x^2\!-\!12x\!+\!36)=\frac{75\pi}{108}(-x^2\!-\!4x\!+\!12)=\frac{75\pi}{108}(x\!-\!2)(-x\!-\!6)\)
Daar we een minimum mogen verwachten voor x tussen 0 en 6, en 2 de enige nulwaarde is van D V die tussen 0 en 6 ligt,
mogen we gerust besluiten
dat x = 2 een maximaal volume oplevert voor de kegel.
Overigens is in dat geval de hoogte van de kegel 6 + 2 = 8.

 Een punt P(x,y) op de omtrek van de ellips met vergelijking \(\boldsymbol{\frac {x^2} {36} + \frac {y^2} {25} =1}\)
laat men wentelen rond de x-as zodat een cirkel ontstaat als grondvlak van een kegel met top T(− 6, 0).
Een punt P(x,y) op de omtrek van de ellips met vergelijking \(\boldsymbol{\frac {x^2} {36} + \frac {y^2} {25} =1}\)
laat men wentelen rond de x-as zodat een cirkel ontstaat als grondvlak van een kegel met top T(− 6, 0).