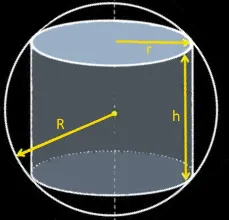
 Een cilinder wordt in een bol met straal
Een cilinder wordt in een bol met straal Wat is de straal r van het grondvlak als die cilinder het grootst mogelijk volume zou moeten hebben ?
 Een cilinder wordt in een bol met straal
Een cilinder wordt in een bol met straal Wat is de straal r van het grondvlak als die cilinder het grootst mogelijk volume zou moeten hebben ? |
A. \(2\) |
|---|---|
| B. \(2\sqrt2\) | |
| C. \(2\sqrt3\) | |
| D. \(\sqrt3\) | |
| E. \(\frac{\sqrt6}{2}\) |
[ 5-8310 - op net sinds 15.11.2017-(E)-5.5.2025 ]
What is het maximum volume of a cylinder that can be inscribed in a shepre of radius R = 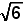 ? ?
|
A. \(2\) |
|---|---|
| B. \(2\sqrt2\) | |
| C. \(2\sqrt3\) | |
| D. \(\sqrt3\) | |
| E. \(\frac{\sqrt6}{2}\) |
