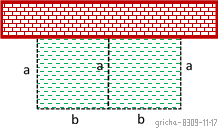
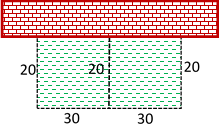
v8309 Een stuk grond, gelegen tegen een gebouw, wil men afbakenen met twee rechthoeken met zijden a en b (zie figuur). Hiervoor heeft men 120 m draad die men volledig benut.
Hoe groot moet de afmeting  a  zijn opdat de oppervlakte van de twee rechthoeken samen, maximaal zou zijn ? 		A.  15
B.  20
C.  24
D.  30
E.  40
A    B    C    D    E

[ 4-8309 - op net sinds 5.2.2019-()-14.11.2024 ]

Translation in   E N G L I S H

IN CONSTRUCTION
max area
120 m   wire

Oplossing - Solution

De oppervlakte  S  van de rechthoeken is   2ab waarbij 3a + 2b = 120
Bijgevolg is   S = a.2b = a(120 − 3a) = 3a(40 − a)
Vermits 3a(40 − a) een kwadratische uitdrukking is, hebben we geen afgeleiden nodig om de maximale waarde van 3a(40 − a) te kennen.
Het is nl. de gemiddelde waarde van de twee nulwaarden 0 en 40, m.a.w. 20
De draad moet dus als volgt gespannen worden :
v8309a >
gricha