Wat is de grootste richtingscoëfficiënt die je kan tegenkomen voor een raaklijn in een punt van die kromme ? (m.a.w. zoek de steilste raaklijn)
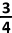
|
Wat is de grootste richtingscoëfficiënt die je kan tegenkomen voor een raaklijn in een punt van die kromme ? (m.a.w. zoek de steilste raaklijn) |
A. 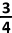 |
|---|---|
| B. 1 | |
| C. 2 | |
| D. 3 | |
| E. 12 |
[ 5-8306 - op net sinds 2.4.2018-()-13.11.2024 ]
| IN CONSTRUCTION |
|---|
