parabool 0 1 2 3 4 1 2 C A B x = k gricha - v8305 - 27.8.2022
De parabool met vergelijking 20y = (x − 8)² raakt de x-as in (8,0). Een verticale rechte  x = k (0 < k < 8) snijdt de parabool in A en de x-as in B.  Met het punt
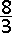
C(0,1) vormt men de ΔABC.
Voor welke waarde van k is de oppervlakte van driehoek ABC het grootst ? 		A.   2
B.   3
C.   3,2
D.   4
E.   8op3
A    B    C    D    E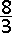

[ 5-8305 - op net sinds 29.3.2018-(E)-4.11.2023 ]

Translation in   E N G L I S H

IN CONSTRUCTION

Maximize area ΔABC
k = ? 		A.  2
B.  3
C.  3,2
D.  4
E.  

Oplossing - Solution

Het is gemakkelijk in te zien dat de oppervlakte S van de driehoek gelijk is aan (1/2  basis × hoogte) :
\(S= \frac12.\frac{(k\,-\,8)^2}{20}.k=\frac{k.(k\,-\,8)^2}{40}=\frac{1}{40}(k^3-16k^2+64k)\)
Het maximum van deze derdegraadsfunctie bepalen we d.m.v. de afgeleide :
\(D_k\;\frac{1}{40}(k^3-16k^2+64k)=\frac{1}{40}(3k^2-32k+64)=\frac{1}{40}(k-8)(3k-8)\)
De enige nulwaarde tussen 0 en 8 is 8/3. Vermits we tussen 0 en 8 een maximum verwachten zal  k = 8/3  ons de maximale oppervlakte voor ABC opleveren. (een eventueel schema kan dat bevestigen)
gricha