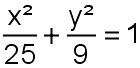P Q F F' 2 -2 -4 -2 2 4 gricha - v8302 - 22.8.2022
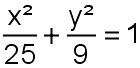In de ellips   snijden de rechten door de brandpunten F en F', loodrecht op de x-as, de ellips in P (boven x-as) en Q (onder de x-as).
Wat is de omtrek van het parallellogram F'PFQ ?		 A.  15
B.  16
C.   6
D.  18
E.  20
A    B    C    D    E

[ 6-8302 - op net sinds 15.4.2018-()-2.11.2023 ]

Translation in   E N G L I S H

IN CONSTRUCTION
circumference of the parallelogram 		A.  15
B.  16
C.   6
D.  18
E.  20

Oplossing - Solution

De halve grote as van de ellips is √25 = 5, zodat 2a = 10.
De definitie van de ellips indachtig zijnde is |F'P| + |PF|
= |F'Q| + |QF| = 2a.   De omtrek is dus 2.10 = 20
Merk op : de loodrechte stand hebben we niet eens gebruikt en was eigenlijk een afleidingsmanoeuvre ! Je kan zelfs het punt P willekeurig kiezen op de ellips (boven de x-as) en Q willekeurig op de ellips (onder de x-as). Zo ontstaat een willekeurige vierhoek waarvan de omtrek nog altijd 20 is !
gricha