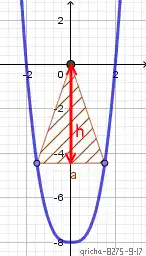
De rechte y = − h (0 < h < 8) snijdt y = |x|³ − 8 in punten waarvan de x-waarden volgen uit − h = |x|³ − 8 ⇔ |x|³ = 8 − h ⇔ \(|x| = \sqrt[3]{8-h}\) ⇔ \(x = \sqrt[3]{8-h}\).
De basis van de driehoek heeft dus een lengte van \(2\sqrt[3]{8-h}\) en de oppervlakte van de driehoek \( S = h\sqrt[3]{8-h}\).
Om een extremum (max.) van S te vinden bereken we de afgeleide van >S naar h :
=D_h\;\left(h.(8-h)^\frac{1}{3}\right)=(8-h)^\frac{1}{3}+h.\frac{1}{3}(8-h)^{-\frac{2}{3}}.(-1))
^\frac{1}{3}-h.\frac{1}{3(8-h)^\frac{2}{3}}=\frac{3(8-h)-h}{3(8+h)^\frac{2}{3}}=\frac{24-3h-h}{3(8+h)^\frac{2}{3}}=\frac{4(6-h)}{3(8+h)^\frac{2}{3}})
Vermits de noemer positief is, is het duidelijk dat in de omgeving van h = 6 de afgeleide van positief (stijgen van S) overgaat naar negatief (dalen van S)
zodat we mogen besluiten dat voor h = 6 de oppervlakte maximaal wordt.
De kromme met vergelijking