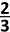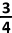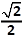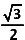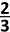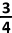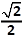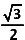De grote basis is gelijk aan 2 (dubbel van de straal). De kleine basis is een koorde die evenwijdig is met de grote basis (middellijn) en door de stelling van Pythagoras een lengte heeft van  \(2\sqrt{1-h^2}\).
De oppervlakte S van het trapezium is bijgevolg \(S = \frac{1}{2}h\left(2\sqrt{1-h^2}+2\right)=h\;\sqrt{1-h^2}+h\).
Om een extremum (minimum) van S te bepalen bereken we de afgeleide van S naar h :
\(D_h\;S\;=D_h\;\left(h\;\sqrt{1-h^2}+h\right)=\sqrt{1-h^2}+h.\frac{-2h}{2\sqrt{1-h^2}}+1=\frac{1-h^2-h^2}{\sqrt{1-h^2}}+1=\frac{1-2h^2}{\sqrt{1-h^2}}+1\)
Nulwaarden verkrijg je door oplossen (in ] 0, 1 [ ) van
\(1=\frac{2h^2-1}{\sqrt{1-h^2}}\;\;\Leftrightarrow\;\;\sqrt{1-h^2}=2h^2-1\;\;\Leftrightarrow\;\;1-h^2=4h^4-4h^2+1\\\;\;\Leftrightarrow\;\;4h^4-3h^2=0\;\;\Leftrightarrow\;\;4h^2-3=0\;\;\Leftrightarrow\;\;\ h^2=\frac{3}{4}\;\;\Leftrightarrow\;\;\ h=\frac{\sqrt3}{2}\)
Als er inderdaad een maximum is voor S (wat de opgave suggereert),
dan kan dit alleen zijn voor een hoogte van  \(\frac{\sqrt3}{2}\approx 0,866\)