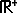Eigenlijk moeten we de volgende ongelijkheid oplossen (in ) :
    log (x⁴ + 5x² − 14 < 1
 ⇔   0 < x⁴ + 5x² − 14) < 10 ,   dus eigenlijk twee ongelijkheden.
We lossen afzonderlijk op :
1)   0 < x⁴ + 5x² − 14       ( 7.(−2) = −14, 7+(−2) = 5 )
  ⇔   0 < (x² + 7).(x² − 2)     nu delen door (x² + 7) (positief!)
  ⇔   0 < x² − 2
  ⇔   x² > 2
  ⇔   x >  ∨  x < −
2)   x⁴ + 5x² − 14 < 10
  ⇔   x⁴ + 5x² − 24 < 0       ( 8.(−3) = −24, 8+(−3)=5 )
  ⇔   (x² + 8).(x² − 3) < 0     nu delen door (x² + 8) (positief!)
  ⇔   x² − 3 < 0
  ⇔   x² < 3
  ⇔   − < x <
De positieve getallen die aan beide ongelijkheden voldoen zijn dus deze waarbij  x >   én   x <   m.a.w.   x ∈ ] ,[