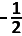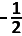[ 4-8224 - op net sinds 10.11.2017-(E)-9.12.2024 ]
Translation in E N G L I S H
If
2.cos 2α + 2.sec 2α = 5,
then 2.cos 4α
equals
|
A. − 1 |
|---|
B. 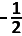 |
C.  |
D.  |
| E. 1 |
Oplossing - Solution
2.cos 2α + 2.sec 2α = 5
⇔ 2.cos² 2α + 2 = 5.cos 2α
⇔ 2.cos² 2α − 5.cos 2α + 2 = 0
⇔ 2.y² − 5.y + 2 = 0 ∧ y = cos 2α
De discriminant van de vierkantsvergelijking is D = 25 − 4.2.2 = 9
zodat y = ¼ (5 ± 3) ⇔ y = 2 ∨ y = ½
cos 2α = 2 heeft geen oplossingen zodat er overblijft : cos 2α = ½
Nu kunnen we verder gaan op twee manieren :
1ste manier :
Daar 1 + cos 2α = 2.cos² α
is 1 + cos 4 α = 2.cos² 2α
en cos 4α = 2.cos² 2α − 1
en 2.cos 4α = 4.cos² 2α − 2 = 4.( ½ )² − 2 = 1− 2 = −1
2de manier :
cos 2α = ½
==> cos 2α = cos 60°
==> 2α = ±60° + k.360°
==> 4α = ±120° + k.720°
==> cos 4α = cos 120°
==> cos 4α = −cos60°
==> cos 4α = − ½
==> 2.cos 4α = − 1